Modeling relationships from themes in text and covariates with an outcome: A Bayesian supervised topic model with covariates

Abstract

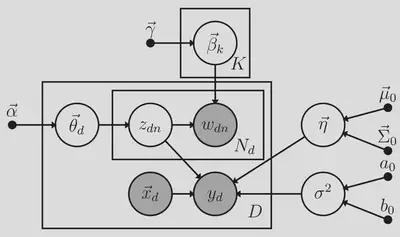
While text analysis has long been of interest in psychology, quantitative approaches tend to rely on predefined dictionaries of words designed to correspond to constructs of interest. However, construction of dictionaries can be time-consuming and dictionary-based methods cannot accommodate relevant words that fall outside the dictionary. Furthermore, dictionary methods typically assign a word to only one construct and fail to account for polysemy and homonymy. One alternative approach, topic modeling, eschews predefined dictionaries and instead models patterns of word co-occurrences using latent categories (i.e., topics). These topics have multiple uses and are often incorporated as components of a subsequent model. In psychological research, unsupervised topic models are typically used to obtain estimated topic proportions as a summary of the text (e.g., to understand the content of survey responses). Associations between these estimated topic proportions and an outcome of interest may be modeled (e.g., in a regression model) as a second stage. However, it is well-known (e.g., in the factor analysis literature) that a two-stage procedure that uses estimated latent variables can be problematic. We propose an extension of the supervised topic model (Blei & McAuliffe, 2008) that jointly estimates a topic model and a regression model to predict an outcome using both the latent topic proportions and other manifest predictors. Our model, supervised latent Dirichlet allocation with covariates (SLDAX), can be fit in a single stage rather than two stages, allows for evaluation of the incremental validity of the topics given other established measures (or vice versa), provides concise summarization of the text, and models relationships between the topics and the outcome. To estimate the SLDAX model, we derived a Markov Chain Monte Carlo sampling algorithm. We also developed an R package, psychtm, that implements SLDAX. Performance of the model for different data characteristics (e.g., number of documents, document lengths, number of topics, presence of covariates) is evaluated in a simulation study. These results are used to make recommendations regarding suggested data requirements for the use of the SLDAX model in applications. Finally, we demonstrate the application of SLDAX on an empirical data set.

Kenneth Tyler Wilcox

Statistical Consultant

My research interests include integrative data analysis, meta-analysis, topic modeling, Bayesian statistics, multilevel modeling, statistical programming, and psychology.