Jointly modeling participant-level data and summary statistics for treatment differences

Cumulative data analysts typically rely on two statistical frameworks: meta-analysis (MA) and integrative data analysis (IDA; Curran et al., 2009). MA analyzes aggregate data (AD, i.e., summary statistics) whereas IDA analyzes individual participant data (IPD). In practice, it is possible that AD are available from some studies whereas IPD are available from others. Recently, two-stage and one-stage multilevel modeling (MLM) approaches have been developed and applied in medical research (e.g., Riley et al., 2008; Papadimitropoulou et al., 2019) to pool AD and IPD. Although jointly modeling AD and IPD may allow for more generalizable and precise estimates, these models remain surprisingly unused in psychological science. Furthermore, analytical examination and small-sample simulation study to evaluate the performance of these models is limited.

We conducted a simulation study to evaluate twelve methods (see Figure 1) for cumulative analysis of treatment differences when (a) only AD, (b) only IPD, and (c) both AD and IPD are available. With only AD, we considered (1) random-effects MA (RMA) and the pseudo-IPD imputation strategy of Papadimitropoulou et al. (2019) with (2) a fixed-intercepts random-slopes (FIRS) MLM, (3) an empirically reference-group mean-centered (RGMC) MLM, and (4) a random-intercepts random-slopes (RIRS) MLM. With only IPD, we considered (1) a FIRS MLM, (2) a RGMC MLM, and (3) a RIRS MLM. With both AD and IPD, we considered (1) the RGMC MLM, (2) the Riley et al. (2008) MLM, and the pseudo-IPD imputation strategy with (3) a FIRS MLM, (4) a RGMC MLM, and (5) a RIRS MLM. To evaluate the estimation accuracy, type I error rate, and power of these approaches with 2-40 AD and/or IPD studies, we generated data from a RIRS MLM for treatment differences with a dichotomous predictor (X, coded zero for the reference group and one for the treatment group) and a normally distributed outcome Y, $$y_{ij}={\gamma }_j+{\theta }_j{x}_{ij}+{ϵ}_{ij},$$ $${\gamma }_j=u_{0j},$$ $${\theta }_j={\mu }_{\theta }+u_{1j},$$ where $x_{ij}$ and $y_{ij}$ are the observed treatment assignment and outcome for participant $i$ in study $j$, respectively, ${\gamma }_j$ and ${\theta }_j$ are the study-specific reference group mean and treatment difference, respectively, and ${\mu }_{\theta }$ is the average treatment difference. Residuals are normally distributed and ${\tau }^2$ is the between-study variance of treatment effects.

Simulation results are summarized in Figure 1. Estimates of ${\mu }_{\theta }$ were ignorably biased in all conditions for all methods. Estimates of ${\tau }^2$ could be negatively biased when a RIRS MLM was fit to IPD with or without imputed pseudo-IPD when the study-level residual correlation was negative. The RGMC MLM yielded positively biased estimates of ${\tau }^2$ with one exception: When the number of AD studies exceeded the number of IPD studies, estimation bias was ignorable.

Despite these cases of biased estimates of ${\tau }^2$, type I error rates for ${\mu }_{\theta }$ were well-controlled with some exceptions. First, RMA was conservative (type I error rates below the nominal rate) with fewer than six (${\tau }^2$ = 0) to 28 studies (“medium” ${\tau }^2$). Second, with at least four studies, all three MLMs produced well-controlled type I error rates with full IPD or pseudo-IPD (for AD and IPD-AD scenarios).

Generally, these results suggest that modeling all available data can improve the estimation precision for ${\mu }_{\theta }$ and power for testing ${\mu }_{\theta }$. Further, modeling IPD—original participant-level data, imputed pseudo-IPD from AD studies, or both—can yield greater precision and power than meta-analysis for ${\mu }_{\theta }$. Notably, analyzing imputed pseudo-IPD from the AD studies in an MLM was noticeably more powerful than RMA (see Figure 2). This may be because an approximate likelihood is used by RMA since the within-study sample variances are treated as known, whereas directly modeling IPD or pseudo-IPD uses an exact likelihood.

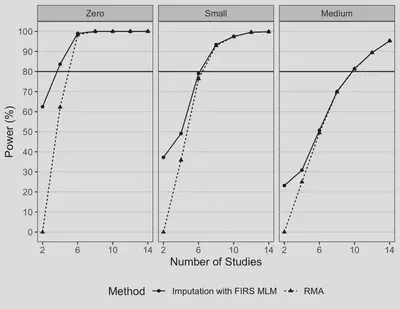
This study introduces novel methods for jointly modeling AD and IPD to psychologists and is the first simulation study to compare these methods. Our results suggest that under correct model specification these models can accurately estimate treatment effects and between-study heterogeneity with AD and/or IPD and improve power by pooling all available data. When both IPD and AD are available, we recommend the Riley et al. (2008) MLM if imputation of pseudo-IPD is not performed. Otherwise, we suggest fitting the FIRS MLM to IPD along with imputed pseudo-IPD if there are available AD studies. When only AD are available, we suggest imputing pseudo-IPD and analyzing it with the FIRS MLM instead of the usual RMA. If covariates are available, we can extend these methods to estimate and test both participant-level and treatment-covariate moderation effects using IPD only or both IPD and AD.

Figure 2. Power Comparison with AD Only for RMA vs. FIRS MLM with Imputed Pseduo-IPD for Testing a “Medium” Average Treatment Effect.

References

Curran, P. J., & Hussong, A. M. (2009). Integrative data analysis: The simultaneous analysis of multiple data sets. Psychological Methods, 14(2), 81–100. https://doi.org/10.1037/a0015914

Papadimitropoulou, K., Stijnen, T., Dekkers, O. M., & Cessie, S. le. (2019). One-stage random effects meta-analysis using linear mixed models for aggregate continuous outcome data. Research Synthesis Methods, 10(3), 360–375. https://doi.org/10.1002/jrsm.1331

Riley, R. D., Lambert, P. C., Staessen, J. A., Wang, J., Gueyffier, F., Thijs, L., & Boutitie, F. (2008). Meta-analysis of continuous outcomes combining individual patient data and aggregate data. Statistics in Medicine, 27(11), 1870–1893. https://doi.org/10.1002/sim.3165