Modeling approaches for cross-sectional integrative data analysis: Evaluations and recommendations
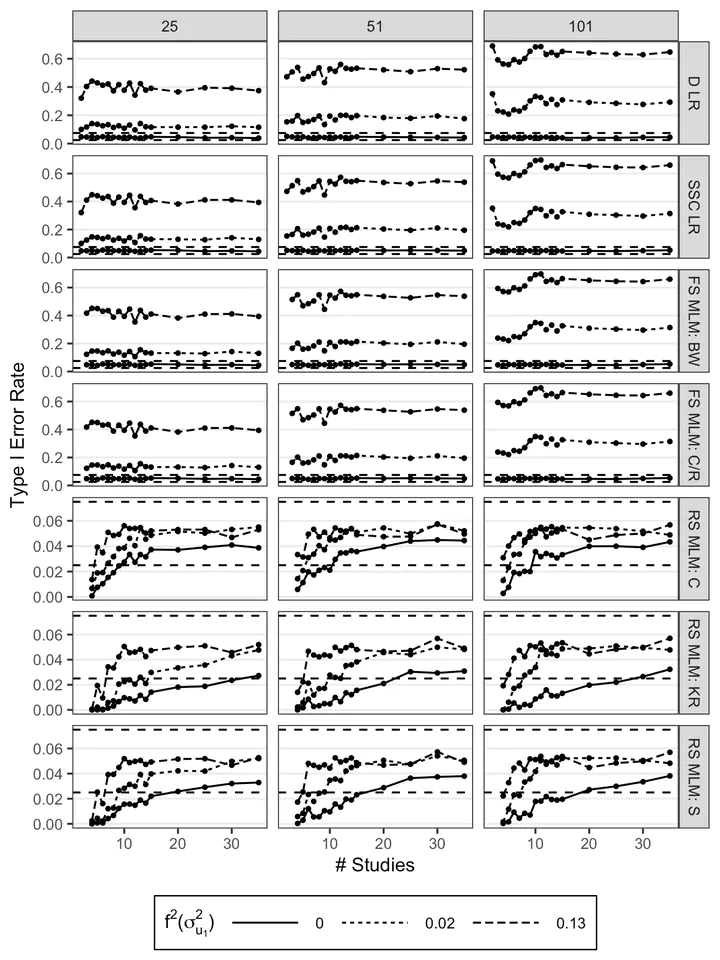Type I error rate for the average participant-level fixed effect, $\gamma_W$, for each model (rows) as a function of the number of studies, the average study sample size (columns), and the effect size of the slope variance $f^2\left(\sigma^2_{u_1}\right)$. Horizontal dashed lines represent upper (0.075) and lower (0.025) bounds for acceptable Type I error rate. D LR = disaggregated linear regression; SSC LR = study-specific coefficients linear regression; FS MLM = fixed-slope MLM; RS MLM = random-slopes MLM; BW = between-within; C/R = containment/residual; KR = Kenward-Roger; S = Satterthwaite.Abstract
Integrative data analysis (IDA) jointly models participant-level data from multiple studies. In psychology, IDA has been conducted using different fixed-effects and multilevel modeling (MLM) approaches. However, evaluations regarding the performance of these models in an IDA context are limited. The goal of this article is to evaluate three fixed-effects models (aggregated vs. disaggregated vs. study-specific coefficients regressions) and two MLMs (fixed-slope vs. random-slopes MLM) for cross-sectional IDA. Using a simulation study with study sample sizes and numbers of studies consistent with applied IDA (e.g., 2–35 studies), we evaluated estimation bias and Type I error rates for participant-level and study-level effects and variance components for these models; for the MLMs, we evaluated different estimation methods (i.e., constrained vs. unconstrained variance estimation and five degrees of freedom methods). Disaggregated and study-specific coefficients regressions and both MLMs yielded fixed effects estimates with ignorable bias, but only the random-slopes MLM fully modeled between-study heterogeneity and, consequently, provided well-controlled Type I error rates for testing both fixed effects. Overall, we found that MLMs could be feasible under IDA conditions with three to six studies and well-chosen estimation methods. A real-data IDA example is used to illustrate and compare the application of the five models. We hope our results will help researchers choose appropriate modeling methods when conducting IDA.
Kenneth Tyler Wilcox
Statistical Consultant
My research interests include integrative data analysis, meta-analysis, topic modeling, Bayesian statistics, multilevel modeling, statistical programming, and psychology.